ප්‍රවේගයකින් චලිතවන වස්තු හමු වීම

ඒකාකාර ප්‍රවේගයෙන් චලනය වන වස්තූන් හමුවීම හෝ ගැටීම සඳහා එක් වස්තුකොට සාපේක්ෂව අනෙක් වස්තුවේ ප්‍රවේගය පළමු වස්තුව දිශාවට තිබිය යුතුය.

වෙනත් ආකාරයකින් කියනවා නම්, කිසියම් මොහොතකදී එම වස්තු දෙක යා කරන රේඛාව ඔස්සේ ක වස්තුව සාපේක්ෂව අනික් වස්තුවේ ප්‍රවේගය තිබිය යුතුය.

පහත සඳහන් උදාහරණ සලකා බලන්න

උදාහරණ 1

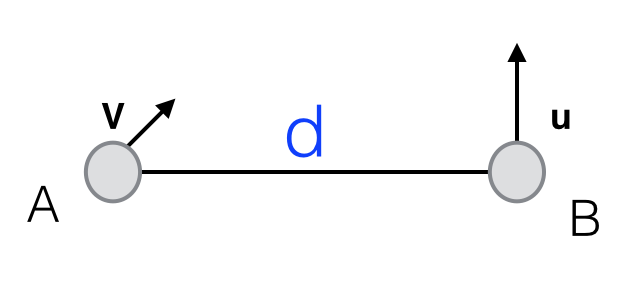
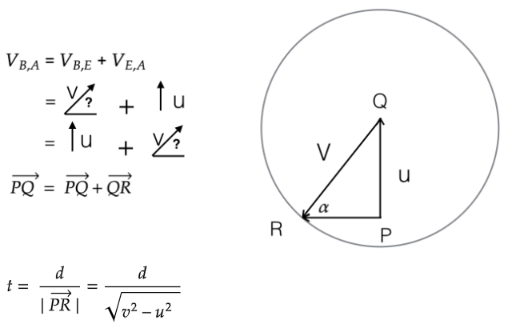
A වස්තුවේ පොළොවට සාපේක්ෂ ප්‍රවේගය v වන අතර B වස්තුවේ පොළොවට සාපේක්ෂ ප්‍රවේගය උතුරු දෙසට u වේ. යම්කිසි මොහොතකදී A ට B පෙනෙන්නේ , හරියටම නැගෙනෙහිර දෙසට d දුරකිනි.

A සහ B එකිනෙක ගැටේ නම්

( a ) A වස්තුවේ දිශාව සොයන්න

( b ) ගැටීමට ගතවන කාලය සොයන්න

a 2021 A/L S නැවක් පොළොවට සාපේක්ෂව u kmh-1 ඒකාකාර වේගයෙන් උතුරු දෙසට යාත්‍රා කරයි. එක්තරා මොහොතකදී, S වලින් d km දුරක් නැගෙනෙහිරින් P බෝට්ටුවක් පිහිටන අතර S වලින් 3 d km දකුණින් වෙනත් Q බෝට්ටුවක් පිහිටයි. P බෝට්ටුව පොළොවට සාපේක්ෂව 2u kmh-1 ඒකාකාර වේගයෙන් සරල රේඛීය පෙතක, S අල්ලා ගැනීමේ අපේක්ෂාවෙන් ගමන් කරන අතර Q බෝට්ටුව පොළොවට සාපේක්ෂව 3u kmh-1 ඒකාකාර වේගයෙන් සරල රේඛීය පෙතක P අල්ලා ගැනීමේ අපේක්ෂාවෙන් ගමන් කරයි. (i) P බෝට්ටුව S නැව අල්ලා ගැනීමට ගතවන කාලය d

3 u h බව ද (ii) Q බෝට්ටුව P බෝට්ටුව අල්ලා ගැනීමට පෙර P බෝට්ටුව S නැව අල්ලා ගන්නා බව ද පෙන්නන්න. 2020 A/L නැවක් පොළවට සාපේක්ෂව u ඒකාකාර වේගයෙන් බටහිර දෙසට යාත්‍රා කරන අතර බෝට්ටුවක් පොළවට සාපේක්ෂව u/2 ඒකාකාර වේගයෙන් සරල රේඛීය පෙතක යාත්‍රා කරයි. එක්තරා මොහොතකදී බෝට්ටුවෙන් d දුරක් උතුරෙන් නැගෙනහිරට 𝜋

3 ක කෝණයකින් නැව පිහිටයි.(i) බෝට්ටුව පොළවට සාපේක්ෂව උතුරෙන් බටහිරට 𝜋

6 කෝණයක් සාදන දිශාවට යාත්‍රා කරයි නම් බෝට්ටුවට නැව අල්ලා ගත හැකි බව පෙන්වා එයට නැව අල්ලා ගැනීමට 2d

3 u ගතවන කාලය බව පෙන්නන්න. (ii) බෝට්ටුව පොළොවට සාපේක්ෂව උතුරෙන් නැගෙනහිරට 𝜋

6 කෝණයක් සාදන දිශාවට යාත්‍රා කරයි නම් නැවට සාපේක්ෂව ඔහුගේ වේගය 7 u

2 බව පෙන්නා නැව සහ බෝට්ටුව අතර කෙටිම දුර d

27 බව පෙන්වන්න. 2019 A/L සමාන්තර ඍජු ඉවුරු සහිත පළල a වූ ගඟක් ඒකාකාර u ප්‍රවේගයෙන් ගලයි. රූපයෙහි A, B, C හා D යන ඉවුරු මත වූ ලක්ෂ්‍ය සමචතුරශ්‍රයක ශිර්ෂ වේ. ජලයට සාපේක්ෂව නියත v (>u) වේගයෙන් චලනය වන B1 හා B2 බෝට්ටු දෙකක් එකම මොහොතක A සිට ඒවායේ ගමන් ආරම්භ කරයි. B1 බෝට්ටුව පළමුව AC දිගේ C වෙත ගොස් ඉන්පසු CD දිශාවට ගඟ දිගේ ඉහලට D වෙත යයි. B2 බෝට්ටුව පළමුව AB දිගේ පහලට B වෙත ගොස් ඉන්පසු BD දිගේ D වෙත යයි.එකම රූපයක B1 හි A සිට C දක්වාද , B2 හි B සිට D දක්වාද චලිත සඳහා ප්‍රවේග ත්‍රිකෝණවල දළ සටහනක් අඳින්න. එනයින්, A සිට C දක්වා චලිතයේදී B1 බෝට්ටුවේ වේගය 1

2(2v2–u2+u) බව පෙන්වා B සිට D දක්වා චලිතයේදී B2 බෝට්ටුවේ වේගය සොයන්න.B1 හා B2 බෝට්ටු දෙකම එකම මොහොතකදී D වෙත ළගා වන බව තවදුරටත් පෙන්වන්න.

ABDCU 2018 A/L පොළවට සාපේක්ෂව ukmh-1 ඒකාකාර වේගයකින් උතුරු දිශාවට නැවක් යාත්‍රා කරයි. එක්තරා මොහොතකදී නැවේ සිට, දකුණෙන් නැගෙනහිරට 𝛽 කෝණයකින් නැවේ පෙතෙහි සිට p km දුරකින් B1 බෝට්ටුවක් නිරීක්ෂණය කරනු ලැබේ. මෙම මොහොතේදීම B2 බෝට්ටුවක් නැවේ සිට බටහිරින් q km දුරකින් නිරීක්ෂණය කරනු ලැබේ. බෝට්ටු දෙකම පොළවට සාපේක්ෂව v (>u) kmh-1 ඒකාකාර වේගයකින් සරල රේඛීය පෙත්වල නැව අල්ලා ගැනීමේ අපේක්ෂාවෙන් යාත්‍රා කරයි. පොළවට සාපේක්ෂව බෝට්ටුවල පෙත් නිර්ණය කිරීම සඳහා ප්‍රවේග ත්‍රිකෝණ වල දළ සටහන් එකම රූපයක අඳින්න. පොළවට සාපේක්ෂව B1 බෝට්ටුවේ පෙත උතුරෙන් බටහිරට 𝛽–sin-1(usin𝛽

v) කෝණයක් සාදන බව පෙන්වා පොළවට සාපේක්ෂව B2 බෝට්ටුවේ පෙත සොයන්න. 𝛽= 𝜋

3 හා v=3 u යැයි ගනිමු, 3q2>8p2 නම්, B1 බෝට්ටුව B2 බෝට්ටුවට පෙර නැව අල්ලා ගන්නා බව පෙන්නන්න. 2017 A/L 2016 A/L පළල A වූ සෘජු ගඟක් ඒකාකාර වූ වේගෙකින් ගලයි. ගඟ ගලන දිශාවට ඒසී රේඛාව ලම්බ වන පරිදි A හා C ලක්ෂය ගඟේ ප්‍රතිවිරුද්ධ ඉවුරු දෙකෙහි පිහිටා ඇත තවද ABC සමපාද ත්‍රිකෝණයක් වන පරිදි AC ගෙන් උඩුගං අතට බෝයාවක් ගඟ මැද සවිකර ඇත. (යාබද රූපය බලන්න) ජලයට සාපේක්ෂව v (>u) වේගයෙන් චලනය වෙන බෝට්ටුවක් A සිට ආරම්භ කර B වෙත ලගාවෙන තෙක් චලනය වේ. ඊලගට එය B සිට C දක්වා චලනය වේ.A සිට B දක්වාත් , B සිට A දක්වාත් චලිත සඳහා ප්‍රවේග ත්‍රිකෝණ එකම රූප සටහනක අඳින්න. A සිට B දක්වා චලිතයේදී බෝට්ටුවේ වේගය 1

2(4v2–u2–3u) බව පෙන්වා BC දක්වා චලිතයේ දී එහි වේගය සොයන්න. එනයින් AB හා BC පෙත් සඳහා බෝට්ටුව ගන්න මුළු කාලය a4v2–u2

v2–u2 බව පෙන්නන්න. 2015 A/L S නැවක් ඒකාකාර වේගයෙන් උතුරු දිශාවට යාත්‍රා කරයි. එහි සරල රේඛීය පෙත P වරායක සිට නැගෙනහිර පැත්තට p ලම්භ දුරකි න් පිහිටා ඇත. එක්තරා මොහොතකදී PS දිශාව නැගෙනහිරෙන් දකුණට අංශක 45 ක කෝණයක් සාදන විට විට දී ම, S නැව හමුවීම සඳහා B1 හා B2 සැපයුම් බෝට්ටු දෙකක් වරායේ සිට වෙනස් දිශා දෙකකට ඒකාකාර වේගයෙන් එක විට ගමන් අරඹයි. මෙම බෝට්ටු පිළිවලින් T1 හා T2 කාල වල දී S නැවට ළගා වේ. v

u=2

3 බව තවදුරටත් වී ඇත්නම් නැවට සාපේක්ෂව B1 හා B2 බෝට්ටු වල චලිත සඳහා සාපේක්ෂ ප්‍රවේග ත්‍රිකෝණ දෙකෙහි දළ සටහන් එකම රූපයක ඇඳ P වරායේ සිට S නැව වෙත ගමන් කිරීමේදී B1 හා B2 බෝට්ටුවල නියම චලිත දිශා සොයන්න. තවදුරටත් T2–T1=23p

3 බව පෙන්වන්න. 2014 A/L සෘජු සමාන්තර ඉවුරු සහිත ගඟක් ඒකාකාර u ප්‍රවේගයෙන් ගලාබසී. A හා B ලක්ෂ්‍ය දෙක එකක් එක් ඉවුරක ද, අනෙක අනෙක් ඉවුරේද පිහිටා ඇත්තේ AB යන්න u සමග 𝛼 සුළු කෝණයක් සාදන පරිදිය. පිරිමි ළමයෙක් A වලින් ආරම්භ කර ජලයට සාපේක්ෂව අචල දිශාවකට විශාලත්වය 2u නියත ප්‍රවේගයකින් පිහිනමින්, B වෙත ළඟා වෙයි. මෙහි u=|u| වේ. ඔහු ඉන්පසු B වලින් ආරම්භ කර A වෙත ආපසු පැමිණෙන පරිදි ජලයට සාපේක්ෂව අචල දිශාවකට එම 2u විශාලත්වය ම සහිත ප්‍රවේගයකින් පිනයි. A සිට B දක්වා චලිතය සඳහා ද B සිට A දක්වා චලිතය සඳහා ද ප්‍රවේග ත්‍රිකෝණවල දළ සටහන් එකම රූපය රූපයක අඳින්න. ඒ නයින් A සිට B දක්වා චලිතය සඳහා ද, B සිට A දක්වා චලිතය සදහා ද ජලයට සාපේක්ෂව ඔහුගේ ප්‍රවේගය පිළිවෙලින් AB හා BA සමඟ එකම 𝜃 කෝණයකින් සෑදීය යුතු බව පෙන්නන්න. මෙහි sin𝜃=1

2sin𝛼 වේ.B සිට A දක්වා පිහිනීමට ගත් කාලය, A සිට B දක්වා පිහිනීමට ගත් කාලය මෙන් k (1<k<3) ගුණයක් නම්, cos𝜃=1

2s(k+1)

(k–1)cos𝛼 බව පෙන්වන්න. sin𝜃 හා cos𝜃 සදහා වු ඉහත ප්‍රකාශන භාවිතයෙන් cos𝛼= (k–1)

23

2 බව පෙන්වන්න 2013 A/L පළල b වු වෑන් රථයක් ඒකාකාර u වේගයෙන් සෘජු පාරක් දිගේ පදිකවේදිකාවට සමාන්තරව එහි ගෑවි නොගෑවී ගමන් කරයි. පිරිමි ළමයෙක් වෑන් රථයට d දුරක් ඉදිරියෙන් පදිකවේදිකාවේ සිට පාරට බැස වෑන් රථයේ චලිත දිශාව සමග 𝛼 සුළු කෝණයක් සාදන දිශාවට v (u<v sec𝛼) ඒකාකාර ප්‍රවේගයෙන් ඇවිද යයි ළමයා වෑන් රථයේ නොගැටී යාන්තමින් බේරේ නම් bu=(bcos𝛼+dsin𝛼)v බව පෙන්නන්න. 2012 A/L දකුණු දිශාවට ඍජු මාර්ගයක් දිගේ u kmh-1 වේගයෙන් දුවන පිරිමි ළමයකුට සුළගක් බටහිර දෙසින් හමා එනු පෙනේ. උතුරු දිශාවට ඍජු මාර්ගයක් දිගේ එම වේගයෙන්ම දුවනවිට ඔහුට සුළග නිරිත දිශාවෙන් හමනු පෙනේ. සුළගේ චලිත සඳහා සාපේක්ෂ ප්‍රවේග වල ත්‍රිකෝණ එකම රූප සටහනක අඳින්න. එනයින් සුළගේ විශාලත්වය හා දිශාව සොයන්න. 2011 A/L පහන් කණු තුනක ඉහළම ලක්ෂය වන A B හා C තිරස් තලයක දිග a වන සමපාද ත්‍රිකෝණයක සමපාද ත්‍රිකෝණයක ශීර්ෂවල පිහිටා ඇත. සුළඟක් සනත v වේගෙන් AC දිශාවට හමා යයි. සුළඟට සාපේක්ෂව v (>u) වේගයක් ඇති කුරුල්ලෙක් AB දිගේ A සිට B දක්වා ද BC දිගේ B සිට C දක්වා ද පියාඹයි. ගමනේ කොටස් දෙක සඳහා සාපේක්ෂ ප්‍රවේග වල ත්‍රිකෝණ එකම රූප සටහනක් අඳින්න. ඒ නයින් A සිට C දක්වා B හරහා වූ ගමන සඳහා ගතවන මුළු කාලය 4a

u+4v2–3u2 බව පෙන්නන්න. 2010 A/L මිනිසෙකුට නිශ්චල ජලයේ u වේගයෙන් පිහිනිය හැකි ය. d පළලින් යුත් ගඟක් පොළවට සාපේක්ෂව v (<u) වේගයෙන් ගලා බසී ගඟෙහි එක් ඉවුරක මත පිහිටි P ලක්ෂයක මිනිසා සිටින අතර ඔහු ගඟ එහි අනික් ඉවුර මත ගඟ ගලන දිශාවට විරුද්ධ දිශාවෙන් පිහිටි Q ලක්ෂයකට පිහිනා ආපසු P ලක්ෂය වෙත පිහිනීමට බලාපොරොත්තු වෙයි. ඉවර සෘජු හා එකිනෙක සමාන්තර ද PQ ගඟ ගලන දිශාවට විරුද්ධ දිශාව සමග 𝛼 (0<𝛼<𝜋

2) කෝණයක් සාදයි ද නම් ප්‍රවේග සාපේක්ෂ වල ප්‍රවේග ත්‍රිකෝණ එකම රූප සටහනක ඇඳීමෙන් හෝ වෙනත් ක්‍රමයකින් හෝ Q ලක්ෂය ට පිහිනා පසු P ලක්ෂයට පිහිනීමට මිනිසාට ගතවන කාලය 2du2cosec2𝛼–v2

u2–v2 බව පෙන්නන්න. (i) Q ලක්ෂ්‍ය P ලක්ෂ්‍යයේ සිට ගඟ ගලන දිශාවේද ගඟ කරන දිශාව සමග 𝛼 (0<𝛼<𝜋

2) කෝණයක් සාදයි නම් ගන්නා මුළු කාලයේ වෙනසක් සිදු නොවන බව (ii) මුළු කාලය අවම වන්නේ P ලක්ෂ්‍යකට සෘජු ලෙස ඉදිරිපසින් අනෙක් ඉවුර මත Q ලක්ෂ්‍යකට පිහිටන විට බව අපෝහනය කරන්න 2009 A/L u kmh-1 වේගයෙන් ගමන් කරන සබ්මැරිනයක් දකුණින් 30° බටහිර දිශාවට d km දුරකින් මුහුදේ වු නැවත් දකියි. එම නැව v kmh-1 ප්‍රවේගයෙන් උතුරට ගමන් කරමින් තිබේ මෙහි u<v<2u වේ. නැවට සාපේක්ෂ සබ්මැරිනයේ චලිතය සැලකීමෙන් නැව අල්ලා ගැනීම සඳහා සබ්මැරිනය දිසා දෙකකින් එකක් ඔස්සේ ගමන් කළ යුතු බව පෙන්වා මෙම දිශා දෙක අතර කෝණය සොයන්න. ඒවාට අනුරූප කාල පැය d4u2–v2

v2–u2 වෙනස් වන බව තවදුරටත් පෙන්වන්න.